Pattern Recognition Practical 1- Modelling and Fitting
5%. To be completed by 30/10/06, to be marked by 20/11/06.
1. Objectives
The aim of this practical is to enhance your understanding of the lectures on modeling and fitting, in particular on: linear modelling, principal components regression, and principal components analysis, using data that you generate yourself to approximate an ellipse.
2. Procedure
Carry out each of the steps listed below and write a brief report containing:
- a description of the
techniques used, where appropriate in succinct mathematical terms,
- a description of what was
done, what data was used, how it was obtained, what Matlab, library
functions and procedures were used,
- the results obtained,
- an analysis and critique of
the results,
- any conclusions you can draw from the exercise.
Include any code you write yourself (suitably commented) in an appendix together with any scripts.
3. Exercises
3.1 Linear Least Squares Problem Formulation
The equation of an ellipse, centred
at 
with semi axes 
and 
may be written in
parametric form as:
. (1)
Choose at random suitable values
of 
in the range [10,16], 
in the range [8,12]
and
and 
. Use MatLab to plot the ellipse for reference.
The ellipse defined by the parametric equations above may be written in implicit form as:
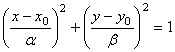. (2)
The semi-axes of ellipse (1) are aligned with the cartesian co-ordinate axes. A more general form for the implicit equation of an ellipse is that of a conic section:
, (3)
which may conveniently be written in matrix-vector form as:
. (4)
If the ellipse is sampled at 
points, 
, so that the design matrix 
is 
with rows
, (5)
the parameter vector 
may be estimated by
means of the least squares solution of the equations
, (6)
where 
is an 
column vector. Thus,
formally:
, (7)
and the minimum squared error is:
. (8)
3.2 Generating the Data
Noisy data samples may be generated by rounding the values
of 
and 
obtained from equation
(1) to the nearest integer.
3.3 Random sampling of the ellipse
Generate 10 pairs of noisy samples 
by choosing values of 
at random in the range
[0,360] and rounding the values ofandobtained as described in 3.2.
Estimate the parameters of the ellipse, explaining what Matlab
functions you use. Compare the results obtained for the parameters of the
ellipse with the parameter values implied by the input values of , , and , plot the ellipse corresponding to your parameter estimates
and compare it with the original ellipse. Calculate the minimum squared error
and comment on your results. Save the matrix 
for future reference.
3.4 Uniform sampling of the ellipse
Generate 10 pairs of noisy samples by choosing values of 
in equation (1)
uniformly over [0,360] according to:
. (9)
and rounding and as indicated above. Compare the results obtained with the
input values of , , and , and with those obtained in 3.3 above. Plot the ellipse
corresponding to your parameter estimates and compare it with the original
ellipse and that obtained in 3.3 above. Calculate the minimum squared error and
comment on your results, in particular, in comparison with those obtained in
3.3 above. Save the matrix for future reference.
3.5 Non-uniform sampling of the ellipse
Repeat the experiment carried out in 3.4 above, but for 10 pairs of noisy samples chosen non-uniformly according to:
. (10)
Compare the results obtained
with the parameter values implied by the input values of ,, and , plot the ellipse corresponding to your parameter estimates
and compare it with the original ellipse and those obtained in 3.3 and 3.4
above. Calculate the minimum squared error and comment on your results, in
particular in comparison with those obtained in 3.3 and 3.4 above. Again, save
the matrix for future reference.
3.6 Sampling a segment of the ellipse
Repeat the experiments carried out in 3.4 and 3.5 above, but for 10 pairs of noisy samples chosen in the range [60,120] degrees, according to:
(i) 
, (11)
and
(ii) 
. (12)
Compare the results obtained
with the parameter values implied by the input values of ,, and , plot the ellipses corresponding to your estimates and
compare them with the original ellipse, with those obtained previously, and
with each other. Similarly, calculate the minimum squared error and comment on
your results. As usual, save the matrices for future reference.
3.7 Effect of changes of origin
Repeat the experiment carried out for the uniformly sampled ellipse as in 3.4 above, but after:
(i)
shifting the center of the ellipse a long way from the
origin by choosing at random in the range
[99, 101] and at random in the range
[-1,1];
(ii)
shifting the center of the ellipse close to the point
(9,0) by choosing at random in the range
[8.9, 9.1] and at random in the range
[-0.1,0.1];
(iii)
shifting the center of the ellipse close to the origin
by choosing and at random in the range [-0.1, 0.1].
Compare the results obtained
with the parameter values implied by the input values of ,, and , plot the ellipses corresponding to your estimates and
compare them with the original ellipses, with that obtained previously in 3.4,
and with each other. As usual, calculate the minimum squared error and comment
on your results. As usual, save the matrices for future reference.
3.8 Stability analysis
Compute the eigenvalues 
of the matrices and make a table of
their values for each of the seven experiments carried out above. Discuss as
quantitatively as you can the significance of the values obtained in relation
to the results of your fitting experiments.
3.9 Ridge regression
Use the results obtained for the
eigenvalues in 3.8 above to investigate how ridge regression might be used to
estimate the parameters of the ellipse in 3.6 (i), 3.7(i) and 3.7(ii) above.
Comment on the results you obtain by means of the ridge regression and the
values of the ridge parameter 
that you use.
3.10 Principle components regression
Use principle components
regression to estimate the parameters of the ellipses in 3.6 (i), 3.7(i) and
3.7(ii) above, by formally setting to zero large values of 
resulting from your diagonalisation of the matrices . Comment on the results you obtain, in particular in
comparison with those originally obtained for these examples and with those
obtained by ridge regression in 3.9 above.
3.10 Estimating the parameter variances and covariances
Comment on the feasibility of estimating the parameter variances and covariances. Note that you are not necessarily asked to carry out the calculations.
3.11 Use of Principal components analysis
Use principal components analysis to estimate the parameters of the ellipse in 3.7(ii) above by using, instead of (3), the equation
. (13)
Include all six of the parameters
in the parameter
vector and normalize it to
one. Comment on the results you obtain and discuss whether this method is
preferable to the linear least squares methods based on equation (3) and used
in 3.3-3.7 above. Discuss whether you think this PCA technique would be a good
method to use in general for ellipse fitting.
4 Reporting
Produce a summary report on paper (in the format indicated in section 2 above), which includes a critical appraisal of the modeling and fitting techniques you have implemented.
5 Commentary
Ellipse fitting is used here primarily as a convenient example of linear modelling. The fitting criteria defined in equations (3) and (13) are thus based on algebraic errors, i.e., the extent to which the equations are not equal to one or to zero, respectively. However, this exercise should also make you aware that ellipse fitting is far from straightforward. Even if algebraic error measures are used, as here, there are several algebraic and statistical subtleties, some of which are causing the effects illustrated here. See the references below, in particular, by Bookstein, for details.
In addition, computing the geometric error, i.e. the shortest or orthogonal distance from a sample point to the best fitting ellipse is difficult for quite deep mathematical reasons related to the properties of their evolutes. Ellipse fitting thus affords plenty of scope for application of non-linear techniques, such as the Levenberg-Marquardt method described later in this course. Ellipse fitting and its extension to higher dimensions, thus contains a range of algebraic, statistical, geometric and computational subtleties and research papers continue to be produced on the subject, right up to the year 2002. If I remember correctly, there is a Matlab function for ellipse fitting based on the method of Boggs et al (1987). It is not needed for this assignment (and won’t enable you to do the exercises as intended).
References
Ahn, S.
J.; Rauh, W., Cho H. S., Warnecke, H.-J., “Orthogonal distance fitting of
implicit curves and surfaces”, IEEE PAMI 24(5), May 2002, pp. 620 –638.
Boggs,
P. T., Bryd, R. H., and Schnabel, R. B., "A stable and efficient algorithm
for nonlinear orthogonal distance regression", SIAM Journal Sci and Stat
Computing, 8(6), 1052-1078, November 1987.
Bookstein , F.L., “Fitting Conic Sections to Scattered Data”, Computer Graphics and
Image Processing, Part 9, 1979, pp56-71.
Fitzgibbon, A., Pilu, M., Fisher, R.B., “Direct
Trans. PAMI, Vol.21, No5, May 1999, pp. 476-480.
Fitzgibbon A.W, Fisher R,B, “A Buyer’s Guide to Conic Fitting”, Proc. BMVC
1995, Vol2, pp. 513-522.
no43, pp. 558-578,1994.
Kanatani, K., “Renormalization for Unbiased Estimation”, In Proc. Fourth Int’l Conf.
Comput. Vision, pp. 599-606,
Lucaks, G., Martin R, Mashall D, “Faithful least Squares Fitting of Spheres, Cylinders,
Cones and Tori for reliable Segmentation”, Lecture Notes on Computer Science, Vol 1,
ECCV 1998, pp. 671-686.
Sampson, P.D., “Fitting Conic Sections to Very Scattered Data”. Computer Graphics and
Image processing, 18, pp. 97-108,1992.
Taubin, G., “Estimation of Planar Curves, Surfaces and Non-Planar Space Curves
defined by Implicit Equations with Applications to edge and range Image Segmentation”,
IEEE T-PAMI, 13(11), pp. 1115-1138, November 1991.
Zhang, Z., “Parameter Estimation Techniques: A Tutorial with Application to Conic
Fitting”, Int. Journal of Computer Vision, April 1996.
Bernard Buxton
October 2006